Fermat ℓittle Theorem (FℓT)
∀ m ∈ N,
1) p prime =>  = m mod (p)
= m mod (p)
Note: Converse False
[Memorize Trick: military police = military in the mode of police]
Note:
p prime, ∀m,
if p | m,
=> m ≡ 0 mod (p) …(1)
=> multiply p times:
 ≡ 0 mod (p) …(2)
≡ 0 mod (p) …(2)
Substitute (1) to (2): m ≡ 0
=> p prime, ∀ m
 ≡ m mod (p)
≡ m mod (p)
=> No need (m, p) = 1 [co-prime]
E.g. (m, p) = (3, 2) =1
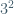 = 9 ≡ 3 mod (2) ≡ 1 mod (2)
= 9 ≡ 3 mod (2) ≡ 1 mod (2)
9 ≡ 1 mod (2)
E.g. (m, p) = (6, 2), p =2 |6
 = 36 ≡ 6 mod (2) ≡ 0 mod (2)
= 36 ≡ 6 mod (2) ≡ 0 mod (2)
6 ≡ 0 mod (2)
WRONG EXAMPLE: p = 4 = non prime
 = 16 ≡ 2 mod (4)
= 16 ≡ 2 mod (4)
but 16 ≡ 0 mod (4)
Equivalent:
p prime => 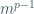 = 1 mod (p)
= 1 mod (p)
by Contra-positive:
3) 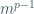 ≠ 1 mod (p)
≠ 1 mod (p)
=> p non-prime
Apply: Prove 39 non-prime?
Take m =2, p= 39
Prove 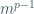 ≠ 1 mod (p)?
≠ 1 mod (p)?
a)  .
.
b)  = 64 ≡ 25 mod (39)
= 64 ≡ 25 mod (39)
c)  = 625 ≡ 1 mod (39)
= 625 ≡ 1 mod (39)
From (b) & (c):
 =
=  ≡
≡  mod(39)≡
mod(39)≡ ≡
≡ ≡ 1
≡ 1
From (a): 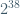 =
= 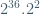 ≡ 1×4 ≠ 1 mod(39)
≡ 1×4 ≠ 1 mod(39)
=> 39 non-prime

